- Overview
- Acoustic Characteristics of the Porous Materials
- Impedance of the system
- Conversion to Absorption Coefficient
- ZORBA User Guide
- References
Overview
The calculation of the absorption coefficient is made in several steps that are described below:
- Determination of the specific impedance and propagation coefficient of the porous materials.
- Calculation of the specific impedance of the system.
- Conversion of the specific impedance into the absorption coefficients, for normal and random incidence, and calculation of the transmission loss.
Every step of the calculation has been the object of an independent study of the scientific literature.
Acoustic Characteristics of the Porous Materials
ZORBA lets the user choose between 9 different models of sound absorption to predict the specific impedance and propagationcoefficient.
Those models are labelled from the name of the researchers that developed them: Allard and Champoux [1], Delany and Bazley, Mechel, Dunn and Davy, Stinson, Beranek, Rayleigh, Wassilief, Allard and Champoux modified.
The Allard and Champoux model is the default model, but Delany and Bazley is also a commonly used model.
Impedance of the system
ZORBA calculates the impedance of the system by simply adding the effect of its different elements, starting with the infinite real impedance of the rigid concrete wall.
From a system whose impedance is , the impedance of this system after the addition of a layer of porous Material whose characteristics are (Specific impedance Z), (Propagation coefficient y) and L (Width) is provided by this formula:
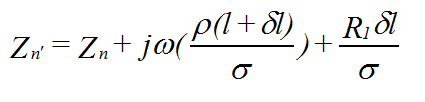
It has been more complicated to find an accurate model of the influence of the different facings. In order to get the best results, our model include some theories of Reynolds, Smith and Kosten [2] to quantify the effects of the distortion of the acoustic field in the areas close to the holes, and a method developed by Mechel [3] to describe the behaviour of this field inside the holes.
Conversion to Absorption Coefficient
The conversion of the specific impedance of the system into normal incidence absorption coefficient is very easy. Let's consider a system which specific impedance is , its normal absorption coefficient is:
![]()
For the Random incidence absorption coefficient, ZORBA's theory is inspired by the work of S.I. Thomasson [4], that not only considers the angle of the propagation of the sound, but also the effect of diffraction at the edge of the absorbent surface.
ZORBA User Guide
The ZORBA User Guide includes advice on getting started with ZORBA modelling. It also contains information about the technical foundations of ZORBA which can assist with developing robust models of sound absorption performance.
The ZORBA Version 3.0 User Guide is accessible here.
References
If you are interested in reading more about the theoretical background that Zorba is based on, the following references provide an excellent introduction.
1. J.F. Allard Y. Champoux, "New empirical equation for sound propagation in rigid frame fibrous material", JASA Vol.91 1992.
2. J.M.A. Smith C.W. Kosten, "Sound absorption by slit resonators", Acustica Vol.1 p 114.
3. F.P. Mechel, "Formulas of acoustics", Ed. Springer.
4. S.I. Thomasson, "Theory and experiments on the sound absorption as function of the area", Report TRITA-TAK-8201, Stockholm may 1982.